2022.06.08 숙제

과제(숙제)

2022.06.08 숙제

디지털 블리자드 2022. 6. 9. 01:19

전위순환 중위순환 후위순환을 정리하세요~!

먼저 TREE 구조는 완전이진트리 구조가 아닌 경우가 많습니다.

완전 이진트리는 배열구조를 사용해도 됩니다.

하지만 완전 이진트리가 아닌경우 배열로 선언하여 사용한다면 메모리 공간 낭비가 심하게되므로 포인터를 사용하여 노드를 구성합니다.

① 전위 순회(Preorder Traversal)

하나의 노드에 방문했을 때 다음의 순서를 따릅니다.

(1) 먼저 자기 자신을 처리합니다.
(2) 왼쪽 자식을 방문합니다.
(3) 오른쪽 자식을 방문합니다.

전위 순회를 이용하면 방문 순서는 다음과 같습니다.

1 - 2 - 4 - 5 - 3 - 6 - 7

② 중위 순회(Inorder Traversal)

하나의 노드에 방문했을 때 다음의 순서를 따릅니다.

(1) 왼쪽 자식을 방문합니다.
(2) 먼저 자기 자신을 처리합니다.
(3) 오른쪽 자식을 방문합니다.

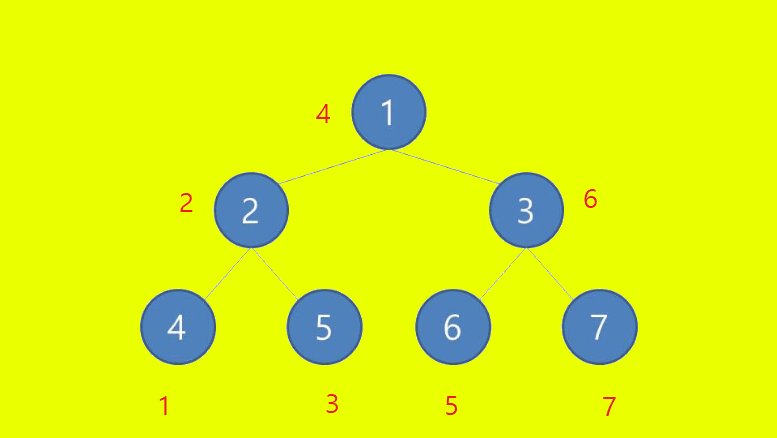
중위 순회는 다음과 같습니다.

4 - 2 - 5 - 1 - 6 - 3 - 7

③ 후위 순회(Postorder Traversal)

(1) 왼쪽 자식을 방문합니다.
(2) 오른쪽 자식을 방문합니다.
(3) 먼저 자기 자신을 처리합니다.

후위 순회는 다음과 같습니다.

4 - 5 - 2 - 6 - 7 - 3 - 1

후위 순회는 주로 계산기 프로그램에 많이 사용됩니다.

===========================================================================

큐와 우선순위 큐란?
큐(Queue)는 먼저 들어오는 데이터가 먼저 나가는 FIFO(First In First Out) 형식의 자료구조입니다.

우선순위 큐(Priority Queue)는 먼저 들어오는 데이터가 먼저 나가기도 하지만, 우선순위가 높은 데이터가 제일 먼저 나가는 형태의 자료구조입니다.

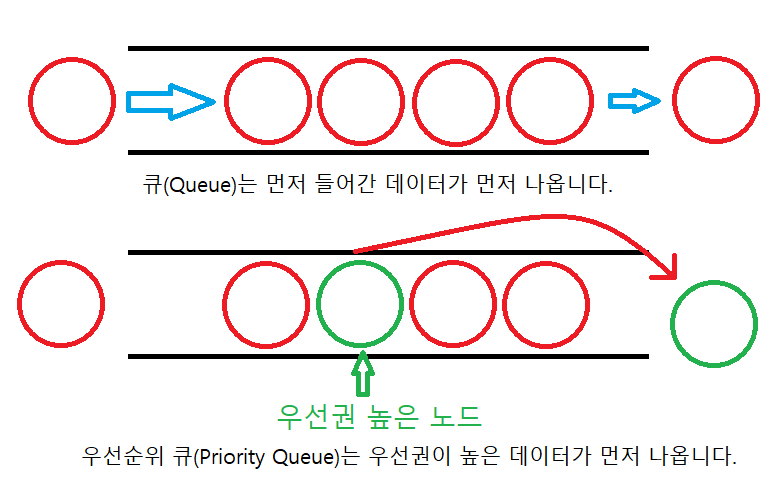
우선순위 큐는 일반적으로 힙(Heap)을 이용하여 구현합니다.

힙 구조란?
힙(Heap)은 우선순위 큐를 위해 고안된 완전이진트리 형태의 자료구조입니다.

힙의 특징은

1. 완전이진트리 형태로 이루어져 있습니다.
2. 부모노드와 서브트리간 대소 관계가 성립됩니다.
3. 이진탐색트리(BST)와 달리 중복된 값이 허용된다.

힙 정렬의 종류는 최대 힙과 최소 힙으로 나뉩니다.
최대 힙 (Max Heap)
부모 노드의 키 값이 자식 노드보다 크거나 같은 완전이진트리입니다.
❝ key(부모노드) ≥ key(자식노드) ❞

최소 힙 (Min Heap)
부모 노드의 키 값이 자식 노드보다 작거나 같은 완전이진트리입니다.
❝ key(부모노드) ≤ key(자식노드) ❞

최대 힙을 예로 들면 아래의 그림은 최대 힙이 형성되지 않았다고 표현합니다.

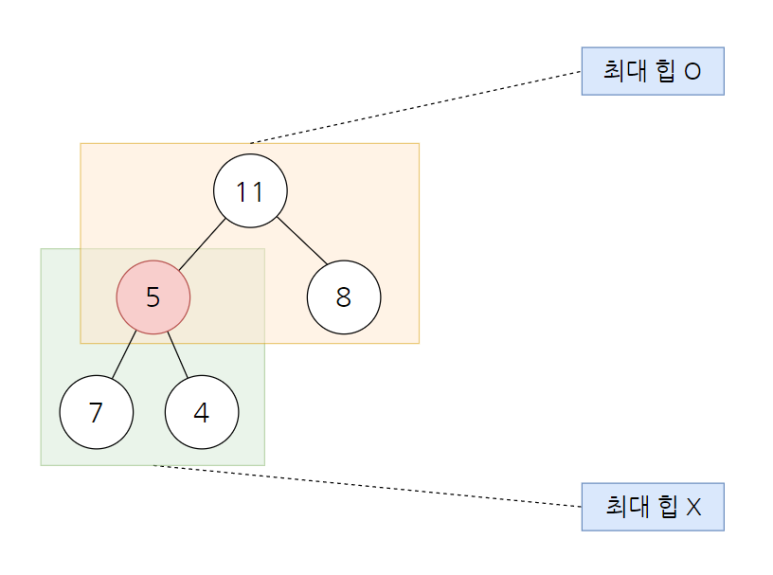
출처 - https://blog.naver.com/ndb796/221228342808

다음 그림은 최대 힙이 형성 되었다고 표현합니다.

힙 정렬의 전체 시간 복잡도는 O(N * log N)입니다.

선택정렬, 버블정렬, 삽입정렬은 시간 복잡도가 O(N^2)입니다.

힙정렬은 위의 정렬들 보다 시간 복잡도가 좋은 알고리즘입니다.

힙정렬 알고리즘 분석해보기

알고리즘 출처 : https://blog.naver.com/ndb796/221228342808

#include <stdio.h>

int number = 9; // 배열의 수
int heap[9] = { 7, 6, 5, 8, 3, 5, 9, 1, 6 }; // 불규칙적인 배열 선언

int main(void) {
// 힙을 구성
for (int i = 1; i < number; i++) {
int c = i; // c 값 : 1 2 3 4 5 6 7 8
do
{

int root = (c - 1) / 2; // root가 가질수 있는 값 0 , 0 , 1 , 1 , 2 , 2 , 3 , 3

if (heap[root] < heap[c])
{
int temp = heap[root];
heap[root] = heap[c];
heap[c] = temp;
}
c = root;

} while (c != 0);
}
// c가 1일때 root = 0
// heap[0] < heap[0] 교체가 일어나지 않음
// c=0이므로 while문 중단됨
//
// c가 2일때 root = 0
// heap[0] < heap[2] 조건문 7 < 5 교체 X
// c=0이므로 while문 중단됨
//
// c가 3일때 root = 1
// heap[1] < heap[3] 조건문 6 < 8 교체 일어남 => { 7, 8, 5, 6, 3, 5, 9, 1, 6 }
// c = 1이므로 while문 허용
// c가 1이되서 root = 0
// heap[0] < heap[1] 조건문 7 < 8 교체 일어남 => { 8, 7, 5, 6, 3, 5, 9, 1, 6 }
// c=0이므로 while 중단됨
//
// c가 4일때 root = 1
// heap[1] < heap[4] 조건문 7 < 3 교체 X
// c = 1 이므로 while문 허용
// c 가 1일때 root = 0
// heap[0] < heap[1] 조건문 8 < 7 교체 X
// c= 0 이므로 while 중단됨
//
// c가 5일때 root = 2
// heap[2] < heap[5] 조건문 5 < 5 교체 X
// c = 2 이므로 while 허용
// c가 2 일때 root = 0
// heap[0] < heap[2] 조건문 8 < 5 교체 X
// c= 0 이므로 while 중단됨
//
// c가 6일때 root = 2
// heap[2] < heap[6] 조건문 5 < 9 교체 일어남 => { 8, 7, 9, 6, 3, 5, 5, 1, 6 }
// c = 2 이므로 while 허용
// c가 2일때 root = 0
// heap[0] < heap[2] 조건문 8 < 9 교체 일어남 => { 9, 7, 8, 6, 3, 5, 5, 1, 6 }
// c= 0 이므로 while 중단됨
//
// c가 7일때 root = 3
// heap[3] < heap[7] 조건문 6 < 1 교체 X
// c = 3 while 허용
// c가 3일때 root = 1
// heap[1] < heap[3] 조건문 7 < 6 교체 X
// c = 1, while 허용
// c가 1일때 root = 0
// heap[0] < heap[1] 조건문 9 < 7 교체 X
// c = 0, while 종료
//
// c가 8일때 root = 3
// heap[3] < heap[8] 조건문 6 < 6 교체 X
// c = 3, while 허용
// c 가 3일때 root = 1
// heap[1] < heap[3] 조건문 7 < 6 교체 X
// c =1, while 허용
// c가 1일때 root = 0
// heap[0] < heap[1] 조건문 9 < 7 교체 X
// c = 0, while 종료
// { 9, 7, 8, 6, 3, 5, 5, 1, 6 }

// 처음 단계가 끝난 후의 모습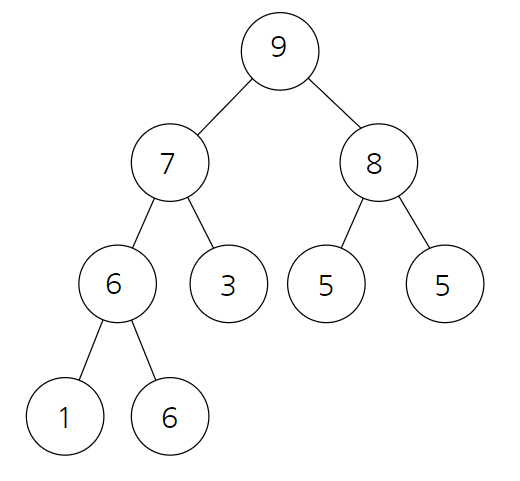

// 크기를 줄여가며 반복적으로 힙을 구성
for (int i = number - 1; i >= 0; i--) {
int temp = heap[0];
heap[0] = heap[i];
heap[i] = temp;
int root = 0;
int c = 1;
do {
c = 2 * root + 1;
// 자식 중에 더 큰 값을 찾기
if (c < i - 1 && heap[c] < heap[c + 1]) {
c++;
}
// 루트보다 자식이 크다면 교환
if (c < i && heap[root] < heap[c]) {
temp = heap[root];
heap[root] = heap[c];
heap[c] = temp;
}
root = c;
} while (c < i);
}

// i가 8일때
// heap[0]과 heap[8]을 자리 바꿈 { 6, 7, 8, 6, 3, 5, 5, 1, 9 }
// root =0, c = 1
// c = 1
// c { 8, 7, 6, 6, 3, 5, 5, 1, 9 }
//
// root = 2, 2 < 8 이므로 while문 허용
// c = 5
// c < i - 1 && heap[5] < heap[6] 조건문 5< 5 X
// c = 5
// c { 1, 7, 6, 6, 3, 5, 5, 8, 9 }
// root = 0 , c = 1
// c = 1
// 조건문 c 1 < 6 and 7 < 6 조건 X
// 조건문 c 1 < 7 and 1 < 7 자리 교체 => { 7, 1, 6, 6, 3, 5, 5, 8, 9 }
// root = 1, 1 < 7 while 허용
// c = 3
// 조건문 c 3 < 6 and 6 < 3 조건 X
// 조건문 c 3 < 7 and 1 < 6 조건 O 자리교체 => { 7, 6, 6, 1, 3, 5, 5, 8, 9 }
// root = 3, 3 < 7 while 허용
// c = 7
// 조건문 작동 X
// 조건문 작동 X
// root = 7 7 < 7 while 중단
//
// i = 6일때
// heap[0]과 heap[6]을 자리 바꿈 => { 5, 6, 6, 1, 3, 5, 7, 8, 9 }
// root = 0 , c = 1
// c = 1
// 조건문 c 1 < 5 and 6 < 6 조건 X
// c = 1
// 조건문 c 2 < 6 and 5 < 6 조건 O 교체 => { 6, 5, 6, 1, 3, 5, 7, 8, 9 }
// root = 1, 1 < 6 while 허용
// c = 3
// 조건문 c 3<5 and 1 < 3 조건 O
C= 4
// 조건문 c 4<6 and 5 < 3 조건 X
// root = 4, 4 < 6 while 허용
// c = 9
// 조건 작동 X
// 조건 작동 X
// root = 9, 9 < 6 while 중단
//
// i = 5일 때
// heap[0]과 heap[5]을 자리 바꿈 => { 5, 5, 6, 1, 3, 6, 7, 8, 9 }
// root = 0 , c = 1
// c = 1
// 조건문 c 1 < 4 and 5 < 6 조건 O
// c=2
// 조건문 c 2<5 and 5 < 6 조건 O 교체 =>{ 6, 5, 5, 1, 3, 6, 7, 8, 9 }
// root = 2 , 2 < 5 while 허용
//
// c = 5
//
// 조건문 5 < 4 and heap[5] < heap[6] => 5 < 4 and 6 < 7 조건 X
// 조건문 5 < 5 and heap[2] < heap[5] => 5 < 5 and 5 < 6 조건 X
// root = 5 , 5<5 while 중단
//
// i=4 일때
// heap[0]과 heap[4]을 자리 바꿈 => { 3, 5, 5, 1, 6, 6, 7, 8, 9 }
// root = 0 , c = 1
// c = 1
// 조건문 c 1<3 and 5 < 5 조건 x
// c = 1
// 조건문 c 1<4 and 3 < 5 조건 O => 교체 => { 5, 3, 5, 1, 6, 6, 7, 8, 9 }
// root = 1 , 1 < 4 while 허용
//
// c = 3
// 조건문 c 3<3 and 5 < 1 조건 x
// 조건문 3 < 5 and heap[1] < heap[3] => 3 < 5 and 5 < 1 조건 X
// root = 3, 3< 4 while 허용
//
//c = 7
// 조건문 작동 X
// 조건문 작동 X
// root = 7, 7< 4 while 중단
//
//
// i = 3 일때
// heap[0]과 heap[3]을 자리 바꿈 => { 1, 3, 5, 5, 6, 6, 7, 8, 9 }
// root = 0 , c = 1
// c = 1
// 조건문 c 1 < 2 and 1 < 3 조건 O
// c = 2
// 조건문 c 2 < 3 and 1 < 5 조건 O => 교체 { 5, 3, 1, 5, 6, 6, 7, 8, 9 }
// root = 2 , 2 < 3 while 허용
//
// c = 5
// 조건 작동 X
// 조건 작동 X
// root = 5, 5 < 3 while 중단
//
// i = 2 일때
// heap[0]과 heap[2]을 자리 바꿈 => { 1, 3, 5, 5, 6, 6, 7, 8, 9 }
// root = 0 , c = 1
// c = 1
// 조건문 c 1 < 1 and 1 < 5 조건 X
// 조건문 c 1 < 2 and 1 < 2 조건 O 교체 =>{ 3, 1, 5, 5, 6, 6, 7, 8, 9 }
// root = 1, 1 < 2 while 허용
// c = 3
// 조건 작동 X
// 조건 작동 X
// root = 3, 3 < 2 while 중단
//
// i= 1 일때
// heap[0]과 heap[1]을 자리 바꿈 => { 1, 3, 5, 5, 6, 6, 7, 8, 9 }
// root = 0 , c = 1
// c = 1
// 조건문 c 1 < 0 and 3 < 5 조건 X
// 조건문 c 1 < 1 and 1 < 3 조건 X
// root = 1, 1 < 1 while 중단
//
// i=0 일때
// heap[0]과 heap[0]을 자리 바꿈 => { 1, 3, 5, 5, 6, 6, 7, 8, 9 }
// 조건 작동 X
// 조건 작동 X
// root = 1, 1 < 0 while 중단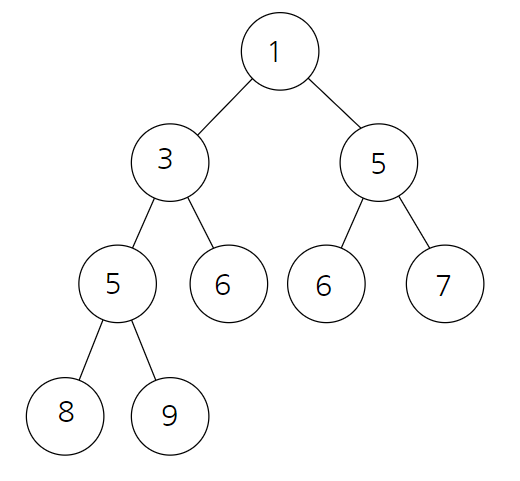
//
//

//
// 최종 결과 => { 1, 3, 5, 5, 6, 6, 7, 8, 9 }
//
// 조만간 그림 삽입
//

// 결과 출력
for (int i = 0; i < number; i++) {
printf("%d ", heap[i]);
}
}

힙 알고리즘 최종결과

{ 1, 3, 5, 5, 6, 6, 7, 8, 9 }

알고리즘 분석결과 첫 단계에서는 자식에서 값들을 비교하여 부모 ROOT 쪽으로 큰 값을 넘겨줍니다.

다음 단계로는 부모의 큰 값들을 맨 끝에있는 자식 노드로 차례로 넘겨줍니다.

그렇게 되면 결과적으로 최소 힙이 완성됩니다.

출처
https ://suyeon96.tistory.com/31
https://blog.naver.com/ndb796/221228342808
https://yunbinni.tistory.com/250
https://blog.naver.com/ndb796/221233560789

저작자표시 비영리 변경금지 (새창열림)

2022.06.08 숙제

전위순환 중위순환 후위순환을 정리하세요~!

① 전위 순회(Preorder Traversal) 하나의 노드에 방문했을 때 다음의 순서를 따릅니다. (1) 먼저 자기 자신을 처리합니다. (2) 왼쪽 자식을 방문합니다. (3) 오른쪽 자식을 방문합니다.

전위 순회를 이용하면 방문 순서는 다음과 같습니다.

1 - 2 - 4 - 5 - 3 - 6 - 7

② 중위 순회(Inorder Traversal) 하나의 노드에 방문했을 때 다음의 순서를 따릅니다. (1) 왼쪽 자식을 방문합니다. (2) 먼저 자기 자신을 처리합니다. (3) 오른쪽 자식을 방문합니다.

중위 순회는 다음과 같습니다. 4 - 2 - 5 - 1 - 6 - 3 - 7

③ 후위 순회(Postorder Traversal) (1) 왼쪽 자식을 방문합니다. (2) 오른쪽 자식을 방문합니다. (3) 먼저 자기 자신을 처리합니다.

후위 순회는 다음과 같습니다. 4 - 5 - 2 - 6 - 7 - 3 - 1

후위 순회는 주로 계산기 프로그램에 많이 사용됩니다.

===========================================================================

우선순위 큐는 일반적으로 힙(Heap)을 이용하여 구현합니다.

다음 그림은 최대 힙이 형성 되었다고 표현합니다.

힙 정렬의 전체 시간 복잡도는 O(N * log N)입니다. 선택정렬, 버블정렬, 삽입정렬은 시간 복잡도가 O(N^2)입니다. 힙정렬은 위의 정렬들 보다 시간 복잡도가 좋은 알고리즘입니다.

힙정렬 알고리즘 분석해보기

① 전위 순회(Preorder Traversal)

하나의 노드에 방문했을 때 다음의 순서를 따릅니다.

(1) 먼저 자기 자신을 처리합니다.
(2) 왼쪽 자식을 방문합니다.
(3) 오른쪽 자식을 방문합니다.

② 중위 순회(Inorder Traversal)

하나의 노드에 방문했을 때 다음의 순서를 따릅니다.

(1) 왼쪽 자식을 방문합니다.
(2) 먼저 자기 자신을 처리합니다.
(3) 오른쪽 자식을 방문합니다.

중위 순회는 다음과 같습니다.

4 - 2 - 5 - 1 - 6 - 3 - 7

③ 후위 순회(Postorder Traversal)

(1) 왼쪽 자식을 방문합니다.
(2) 오른쪽 자식을 방문합니다.
(3) 먼저 자기 자신을 처리합니다.

후위 순회는 다음과 같습니다.

4 - 5 - 2 - 6 - 7 - 3 - 1

힙 정렬의 전체 시간 복잡도는 O(N * log N)입니다.

선택정렬, 버블정렬, 삽입정렬은 시간 복잡도가 O(N^2)입니다.

힙정렬은 위의 정렬들 보다 시간 복잡도가 좋은 알고리즘입니다.